Lady or tiger? | Science game

In trying to prove that irrational numbers are countable, George Cantor found evidence that they are not. Saving the (enormous) distances, when trying to construct the hypothetical “Egyptian tetrahedron” from last week, I found simple and very visual/obvious proof that it is impossible. In fact, the simplest way to construct said tetrahedron (mentally) is to start from a 3×4 rectangle and fold it along the diagonal until the corresponding vertices are 5 units apart. But the important point is that they are already at that distance (since the diameter is measured to an accuracy of 5 units), which would decrease when the rectangle is doubled, thus showing that the supposed Egyptian tetrahedron is a flat shape, and that the faces of the equilateral tetrahedron can only be acute triangles . The impossible Egyptian tetrahedron is the limit of the gradual flattening of an equilateral tetrahedron in which one of the angles of its faces is inclined to 90 degrees.

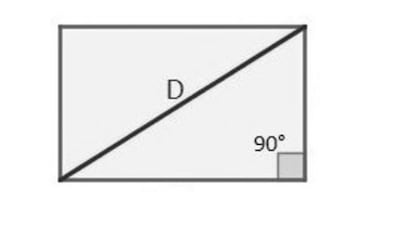
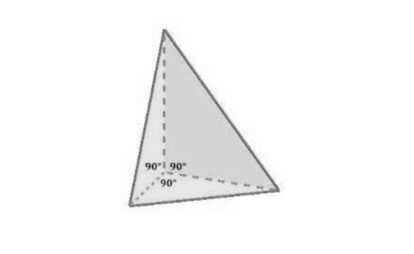
The existing shape is the trirectangular tetrahedron or trirectangular tetrahedron, which is the shape in which the three angles of the faces converging at the vertex are right angles. Thus the three edges that converge at that vertex are the legs of the aforementioned faces, which are clearly right triangles, and the three hypotenuses are the sides of the larger face of the rectangular tetrahedron, which is called the base (regardless of its position). tetrahedral). Can you find the perpendicular height to the base of a triangular tetrahedron based on its three legs? And the size? And the base area?

As a icing on the cake, there’s an elegant problem proposed by Salva Foster: Given an isosurface tetrahedron whose faces are isosceles triangles, find the minimum volume of the sphere containing it, given that the volume of the tetrahedron is an integer.

Problematic decisions

In recent episodes we have seen some problems and paradoxes related to decision theory (see Ellsberg’s paradox and Simpson’s paradox), so it does not hurt to remember the famous story of Frank R. Stockton Lady or tiger?, was published in 1882 and has since been frequently cited when talking about decision making and free will. The story, very briefly, is as follows:

The protagonist has to choose between two doors: behind one is a hungry tiger and behind the other is a beautiful young woman whom he will have to marry. The protagonist’s lover knows which door the tiger is behind. He doesn’t want to see his lover devoured by the monster, but he also can’t bear the thought of seeing him married to his beautiful rival, and he knows it. Indicate with a marker which door he should open. what’s he doing?

Inspired by this disturbing story, Raymond Smulyan, the great contemporary master of logical puzzles, published a hundred years later – in 1982 – a delicious book with the same title, in which you have to overcome a lot of serious tests such as the following:

There are two types of doors. There is a sign that says: “At least behind one of these doors there is a lady.” In the second part, there is a sign that says: “There is a tiger behind the other door.” Knowing that the two verses are either true or both are false, which chapter do you choose?

There are three doors. The sign says: “Behind this door there is a tiger.” The second part says: “Behind this door is a lady.” The person in the third part says: “Behind the second door there is a tiger.” Knowing that at most one of the three signs tells the truth, which door would you choose?

In both cases, you are supposed to prefer the lady over the tiger.

You can follow Theme in Facebook, s And Instagramor sign up here to receive Our weekly newsletter.

_